|
Getting your Trinity Audio player ready...
|
Google Compute Engine or GCE is Google’s IaaS offering in the increasingly crowded cloud computing market. It started its operations in 2013. It makes it easy for you to have access to virtual machines that deliver large amounts of computing power in a cost-effective, secure cloud environment which spans 24 Google Cloud regions.
Compute engine is one of the three core services that are available out of any cloud platform, be it GCP, Azure or AWS.
Those services are: Virtual Machines, Code & Containers, and Serverless

- Since this service from Google is new, they decided to go head-to-head Amazon’s EC2 instances (which started in 2006) and others by keeping a novel billing model that differs somewhat from the norm just to attract customers.
- Each VM is charged for a minimum of [an initial] 10 minutes followed by 1 minute increments, rounded up to the nearest minute.
- Google also throws in sustained-use pricing, in which the hourly rate is tiered downwards the more you use the virtual machine in a given month.
- At 100% usage in a month for example, a customer will have saved 30% on the baseline rates.
- “You pay for what you use” – if you know your usage up-front, you can take advantage of Committed Use Discount which saves up to 57% savings without any up-front costs.
- GCP is used by companies like Spotify, HSBC, Snapchat, Philips, Domino’s, Coco Cola, HTC, etc.
Advantages over Amazon’s EC2 instances
- Google’s instances start up much faster than Amazon’s, by a factor about 60-80%
- At the entry level, an Amazon m1.medium instance (1 CPU, 3.75 GB RAM) cost US$0.12/hour while a similar GCE n1-standard1 instance (1 CPU, 3.75 GB RAM) cost US$0.10/hour.
- At the high end, an Amazon m3.2xlarge VM (8 cores, 30 GB RAM) cost US$0.90/hour, while the similar GCE n1-standard8 cost US$0.83/hour
When to use GCE?
Compute Engine is great for when you need more control of the underlying infrastructure. You might want to use this when:
- You are migrating your apps from on-premises servers or from another cloud service.
- You want to run Windows or other 3rd party applications where you are bringing your own license (BYOL) to CGP or use a license-included VM image. These include ones available in the GCP Marketplace.
- You have a highly customized business logic or you want to run your own storage system.
- You want to have the choice of preset or custom machine sizes that most closely resemble your on-premise structure to best support your workloads.
Machine Types
Google Cloud offers a wide range of Compute Engine machine types. These include:
- General-purpose (N1, N2, N2D and E2) machines that offer the best price-performance ratio. Uses: Web-servers, databases
- Memory-optimized (M2) VMs that offer higher memory per core, up to 12 TB. Uses: In-memory databases, SAP Hana, In-memory analytics
- Compute-optimized (C2) machines that offer the highest performance per core for compute-intensive workloads. Uses: Gaming, High performance gaming
- Accelerator optimized (A2) machines are based on the A100 GPU, for very demanding applications. Uses: Machine learning, Medical analysis
- Shared-core machines for N1 and E2 VMs for a cost-effective way to run small, non-resource-intensive applications.
You also can use what are known as preemptible VMs. These are low-cost, short-term instances that are ideal for running batch jobs and fault-tolerant workloads. Google Cloud indicates that these VMs cut budgets up to 80% over traditional VMs but offer the same performance and capabilities for short-term use.
Reference for machine types: https://cloud.google.com/compute/docs/machine-types
Regions and Zones
Certain Compute Engine resources live in regions or zones. A region is a specific geographical location where you can run your resources. Each region has one or more zones. For example, the us-central1 region denotes a region in the Central United States that has zones us-central1-a, us-central1-b, us-central1-c, and us-central1-f.

Reference for regions and zones: https://cloud.google.com/compute/docs/regions-zones#available
GPUs
Compute Engine provides graphics processing units (GPUs) that you can add to your virtual machine instances. You can use these GPUs to accelerate specific workloads on your instances, such as machine learning and data processing.
You know the ones — those that are computationally intensive, such as machine learning, 3D visualization or medical analysis, to name just a few. GPU accelerators can speed things up on an as-needed basis. Add them to your VMs for these types of workloads and remove them when you are done. You pay only for the time when you are using the resources.
Reference for GPUs: https://cloud.google.com/compute/docs/gpus
CPU platforms
When you start a VM instance on Compute Engine, the instance uses one of the CPU platforms available on Compute Engine. A CPU platform is one of the available CPU processors described in the table below. Compute Engine offers both Intel and AMD processors for your VMs.
Reference for CPU platforms: https://cloud.google.com/compute/docs/cpu-platforms
VM Instance Life Cycle
An instance can transition through many instance states as part of its life cycle. When you first create an instance, Compute Engine provisions resources to start the instance. Next, the instance moves into staging, where it’s prepared for the first boot before it finally boots up and is considered running. A repairing instance is when it goes maintenance. A running instance can be stopped and restarted repeatedly during its lifetime.
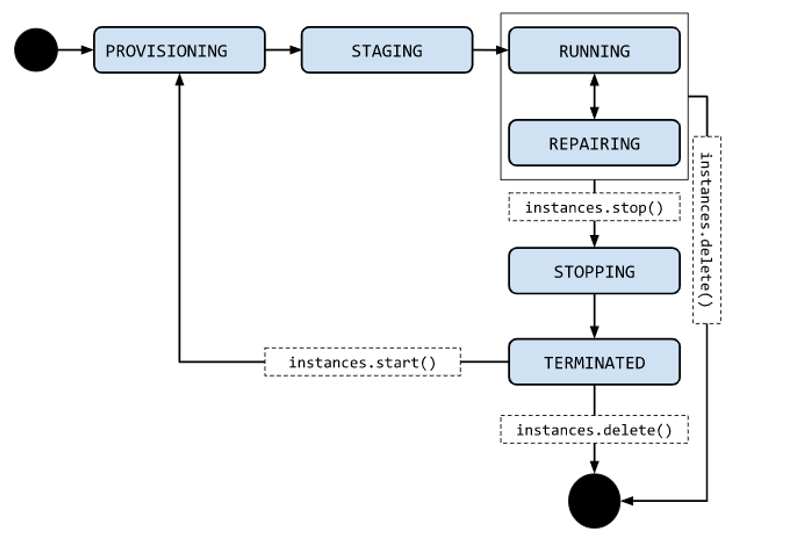
Preemptible VMs
A preemptible VM is an instance that you can create and run at a much lower price than normal instances. However, Compute Engine might terminate (preempt) these instances if it requires access to those resources for other tasks. Preemptible instances are excess Compute Engine capacity, so their availability varies with usage.
If your apps are fault-tolerant and can withstand possible instance preemptions, then preemptible instances can reduce your Compute Engine costs significantly. For example, batch processing jobs can run on preemptible instances. If some of those instances terminate during processing, the job slows but does not completely stop. Preemptible instances complete your batch processing tasks without placing additional workload on your existing instances and without requiring you to pay full price for additional normal instances. You can save up to 80% of the costs.
Reference for Preemptible VMs: https://searchcloudcomputing.techtarget.com/definition/Google-Preemptible-VM-PVM
Creating a VM instance
Step 1: Go to the GCP console link and click on Console.

Step 2: On the top left corner you will have a drop-down option. It has a by default project selected. Click on it to explore more options. I created a project – My First Project

Step 3: Click on the drop-down option on the top left corner and select the Compute Engine Option.
Step 4: Click on create an instance to create the same.


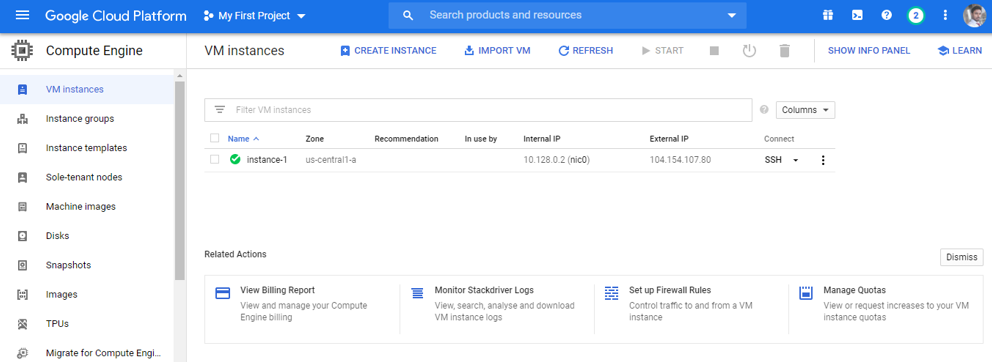
Step 5: Your instance is created.
Similarly, you can create VM instances via CLI.
Conclusion
Infrastructure as a Service (IaaS) is the most important cloud computing vertical. Hence, compute engine gives you full control over infrastructure and direct access to Network / other Compute Services. Google’s current offerings in this space are both cheaper and better-performing than Amazon’s, with the cherry on top being a refreshingly simpler pricing structure that gets cheaper as you use it more.
If this article provided you with value, please support my work — only if you can afford it. You can also connect with me on X. Thank you!




Comments are closed.